কোয়ান্টাম সংখ্যা
যে সংখ্যা দ্বারা অরবিটের আকার, উপশক্তিস্তরের আকৃতি, অরবিটালের ত্রিমাত্রিক অবস্থান ও ইলেকট্রনের ঘূর্ণন প্রকাশ করা হয় তাকে কোয়ান্টাম সংখ্যা বলে।কোয়ান্টাম সংখ্যা বর্তমানে বহুল আলোচিত একটি বিষয়৷ কোয়ান্টাম সংখ্যা ছাড়া অণু-পরমাণু সর্ম্পকে জ্ঞান অর্জন সম্ভব নয়।
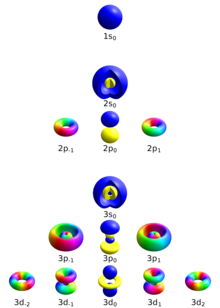
কোনো একটি ইলেকট্রন কোন শক্তিস্তরে আছে, শক্তি স্তরটি বৃত্তাকার না উপবৃত্তাকার এবং ইলেকট্রনটি নিজ অক্ষের চতুর্দিকে ঘড়ির কাটার দিকে না বিপরীত দিকে আবর্তন করে, এসব বিষয় প্রকাশের জন্য কয়েকটি সংখ্যা অবতরণ করা হয়। এ সংখ্যা সমূহই কোয়ান্টাম সংখ্যা নামে পরিচিত।
কোয়ান্টাম সংখ্যার প্রকারভেদ
সম্পাদনা১. প্রধান কোয়ান্টাম সংখ্যা (n) [Principle quantum number]
সম্পাদনা- যে কোয়ান্টাম সংখ্যার সাহায্যে পরমাণুতে অবস্থিত ইলেকট্রনের শক্তিস্তরের আকার নির্ণয় করা যায় তাকে প্রধান কোয়ান্টাম সংখ্যা বলে। একে n দ্বারা প্রকাশ করা হয়,n এর মান যথাক্রমে 1,2,3,4,..... প্রভৃতি পূর্ণ সংখ্যা। প্রধান কোয়ান্টাম সংখ্যার মান বৃদ্ধি হলে নিউক্লিয়াস হতে প্রধান স্তরের দূরত্ব এবং শক্তিস্তরের আকার বৃদ্ধি পায়। বোর মতবাদ অনুসারে n=1 হলে ১ম শক্তিস্তর বা K শেল, n=2 হলে ২য় শক্তিস্তর বা L শেল, n=3 এবং n=4 হলে M ও N ইত্যাদি বোঝায়। যে কোনো প্রধান শক্তিস্তর সর্বোচ্চ 2n² ইলেকট্রন ধারণ করতে পারে (বোরের মতবাদ অনুসারে)।
| n এর মান | প্রতীক |
|---|---|
| ১ | K |
| ২ | L |
| ৩ | M |
| ৪ | N |
| ৫ | O |
| ৬ | P |
| ... | ... |
২. অ্যাজিমুথাল বা সহকারী কোয়ান্টাম সংখ্যা (ℓ) [Azimuthal or subsidiary quantum number]
সম্পাদনা- যা (কৌণিক ভরবেগ কোয়ান্টাম সংখ্যা বা অরবিটাল কোয়ান্টাম সংখ্যা, সহকারী কোয়ান্টাম সংখ্যা) নামেও পরিচিত, সাবশেলকে বর্ণনা করে এবং সম্পর্কের মাধ্যমে অরবিটাল কৌণিক ভরবেগের মাত্রা দেয়।
L2 = ħ2 ℓ (ℓ + 1) রসায়ন এবং বর্ণালীবিদ্যায়, ℓ = 0 কে s অরবিটাল, ℓ = 1, p অরবিটাল, ℓ = 2, d অরবিটাল এবং ℓ = 3, f অরবিটাল বলা হয়।
ℓ এর মান 0 থেকে n −1 পর্যন্ত, তাই প্রথম p অরবিটাল (ℓ = 1) দ্বিতীয় ইলেকট্রন শেলে (n = 2) প্রদর্শিত হয়, প্রথম d অরবিটাল (ℓ = 2) তৃতীয় শেলে (n = 2) প্রদর্শিত হয় = 3), এবং তাই:[2]
ℓ = 0, 1, 2,..., n −1 n = 3, ℓ = 0 থেকে শুরু হওয়া একটি কোয়ান্টাম সংখ্যা, একটি পরমাণুর তৃতীয় ইলেকট্রন শেলের s কক্ষপথে একটি ইলেকট্রনকে বর্ণনা করে। রসায়নে, এই কোয়ান্টাম সংখ্যাটি অত্যন্ত গুরুত্বপূর্ণ, কারণ এটি একটি পারমাণবিক কক্ষপথের আকৃতি নির্দিষ্ট করে এবং রাসায়নিক বন্ধন এবং বন্ধন কোণকে দৃঢ়ভাবে প্রভাবিত করে। আজিমুথাল কোয়ান্টাম সংখ্যাটি একটি কক্ষপথে উপস্থিত কৌণিক নোডের সংখ্যাও নির্দেশ করতে পারে। উদাহরণস্বরূপ, p অরবিটালের জন্য, ℓ = 1 এবং এইভাবে একটি p অরবিটালে কৌণিক নোডের পরিমাণ হল 1।
অরবিটালের আকৃতি আজিমুথাল কোয়ান্টাম সংখ্যা দ্বারাও দেওয়া হয়।
৩. চৌম্বকীয় কোয়ান্টাম সংখ্যা (m) [Magnetic quantum number]
সম্পাদনা- যে সকল কোয়ান্টাম সংখ্যার সাহায্যে ইলেকট্রনের কক্ষপথের ত্রিমাত্রিক দিক বিন্যাস প্রকরণ সমূহ প্রকাশ করা হয়, তাকে ম্যাগনেটিক কোয়ান্টাম সংখ্যা বা চুম্বকীয় কোয়ান্টাম সংখ্যা বলে। চুম্বকীয় কোয়ান্টাম সংখ্যা, m এর মান - l থেকে + l এর পর্যন্ত পূর্ণসংখ্যা। নন-ডিজেনারেট অবস্থায় অরবিটালসমূহ সমশক্তির, তবে চৌম্বকক্ষেত্রে রাখলে শক্তির পার্থক্য তৈরি হয়। আর বলা বাহুল্য, z অক্ষ বরাবর অরবিটাল, যেমন pz, dz² এর বেলায় m=0
s p d f অরবিটাল গুলোর জন্য চৌম্বকীয় কোয়ান্টাম সংখ্যাগুলোর লিখিত আকার হলো:
- s অরবিটালে কেবল 1টি মাত্র ত্রিমাত্রিক বিন্যাস সম্ভব।
- p অরবিটালের জন্য Px Py Pz ( অর্থাৎ সমশক্তি সম্পন্ন 3টি অরবিটাল আছে)
- d অরবিটালের জন্য
dxy dyz dzx dx²-y² dz² (অর্থাৎ সমশক্তি সম্পন্ন 5টি অরবিটাল আছে)
- f অরবিটালের জন্য
fz³ fyz² fxz² fxyz fz(x²-y²) fy(3x²-y²) fx(x²-3y²) (অর্থাৎ সমশক্তি সম্পন্ন 7টি অরবিটাল আছে)
# l এর মনের জন্য m এর মান =(2xl+1)
l= 2 হলে, m এর মান (2×2+1)=5, অর্থাৎ d অরবিটাল। l= 1 হলে, m এর মান (2×1+1)=3, অর্থাৎ p অরবিটাল।
৪. ঘূর্ণন কোয়ান্টাম সংখ্যা (s) [Spin quantum number]
সম্পাদনা- নিজস্ব অক্ষের চারদিকে ইলেকট্রনের ঘুর্ণনের দিক প্রকাশক কোয়ান্টাম সংখ্যা সমূহকে স্পিন কোয়ান্টাম সংখ্যা বা ঘূর্ণন কোয়ান্টাম সংখ্যা বলে। এই কোয়ান্টাম সংখ্যা, s, ফার্মিয়ন কণার বেলায় তা ±½ এর গুণিতক। ইলেক্ট্রনের বেলায় তা ½। +½ ও -½ এর মধ্যে যেকোনো একটিকে ঘড়ির কাটার দিকে ঘূর্ণায়মান ও অপরটি ঘড়ির কাটার বিপরীত অভিমুখে ঘূর্ণায়মান । এটিকে upspin ও downspin electrons ও বলা হয়।
সংক্ষিপ্ত রূপ
সম্পাদনাকোয়ান্টাম উপস্তরের শক্তিক্রম
সম্পাদনাঅরবিট
সম্পাদনাবোরের পরমাণুবাদ মতে নিউক্লিয়াসের চারপাশে ইলেকট্রন কতগুলো অনুমোদিত গোলাকার কক্ষপথে/শক্তিস্তরে আবর্তিত হয় । এদের অরবিট বা কক্ষপথ বলে। প্রতিটি শক্তিস্তরে নির্দিষ্ট সংখ্যক (2n2) ইলেকট্রন থাকে। কোয়ান্টাম মতবাদের উপর ভিত্তি করেই অরবিটের ধারণা প্রতিষ্ঠিত।
অরবিটাল
সম্পাদনাপরমাণুর ভেতর যে ত্রিমাত্রিক জায়গা জুড়ে ইলেকট্রনকে পাবার সম্ভাবনা বেশি, তাকে অরবিটাল বা কক্ষক বলা হয় ।
শক্তিস্তরে ইলেক্ট্রন সংখ্যা অনুসারে মৌলিক পদার্থের তালিকা
সম্পাদনা| পারমাণবিক সংখ্যা | মৌল | প্রতি শক্তিস্তরে ইলেক্ট্রন সংখ্যা | শ্রেণী |
|---|---|---|---|
| ১ | হাইড্রোজেন | ১ | ১ |
| ২ | হিলিয়াম | ২ | ১৮ |
| ৩ | লিথিয়াম | ২, ১ | ১ |
| ৪ | বেরিলিয়াম | ২, ২ | ২ |
| ৫ | বোরন | ২, ৩ | ১৩ |
| ৬ | কার্বন | ২, ৪ | ১৪ |
| ৭ | নাইট্রোজেন | ২, ৫ | ১৫ |
| ৮ | অক্সিজেন | ২, ৬ | ১৬ |
| ৯ | ফ্লোরিন | ২, ৭ | ১৭ |
| ১০ | নিয়ন | ২, ৮ | ১৮ |
| ১১ | সোডিয়াম | ২, ৮, ১ | ১ |
| ১২ | ম্যাগণেসিয়াম | ২, ৮, ২ | ২ |
| ১৩ | অ্যালুমিনিয়াম | ২, ৮, ৩ | ১৩ |
| ১৪ | সিলিকন | ২, ৮, ৪ | ১৪ |
| ১৫ | ফসফরাস | ২, ৮, ৫ | ১৫ |
| ১৬ | সালফার | ২, ৮, ৬ | ১৬ |
| ১৭ | ক্লোরিন | ২, ৮, ৭ | ১৭ |
| ১৮ | আর্গণ | ২, ৮, ৮ | ১৮ |
| ১৯ | পটাশিয়াম | ২, ৮, ৮, ১ | ১ |
| ২০ | ক্যালসিয়াম | ২, ৮, ৮, ২ | ২ |
| ২১ | স্ক্যানডিয়াম | ২, ৮, ৯, ২ | ৩ |
| ২২ | টাইটানিয়াম | ২, ৮, ১০, ২ | ৪ |
| ২৩ | ভ্যানাডিয়াম | ২, ৮, ১১, ২ | ৫ |
| ২৪ | ক্রোমিয়াম | ২, ৮, ১৩, ১ | ৬ |
| ২৫ | ম্যাঙ্গানিজ | ২, ৮, ১৩, ২ | ৭ |
| ২৬ | আয়রন | ২, ৮, ১৪, ২ | ৮ |
| ২৭ | কোবাল্ট | ২, ৮, ১৫, ২ | ৯ |
| ২৮ | নিকেল | ২, ৮, ১৬, ২ | ১০ |
| ২৯ | কপার | ২, ৮, ১৮, ১ | ১১ |
| ৩০ | জিংক | ২, ৮, ১৮, ২ | ১২ |
| ৩১ | গ্যালিয়াম | ২, ৮, ১৮, ৩ | ১৩ |
| ৩২ | জার্মেনিয়াম | ২, ৮, ১৮, ৪ | ১৪ |
| ৩৩ | আর্সেনিক | ২, ৮, ১৮, ৫ | ১৫ |
| ৩৪ | সেলেনিয়াম | ২, ৮, ১৮, ৬ | ১৬ |
| ৩৫ | ব্রোমিন | ২, ৮, ১৮, ৭ | ১৭ |
| ৩৬ | ক্রিপ্টন | ২, ৮, ১৮, ৮ | ১৮ |
| ৩৭ | রুবিডিয়াম | ২, ৮, ১৮, ৮, ১ | ১ |
| ৩৮ | স্ট্রনশিয়াম | ২, ৮, ১৮, ৮, ২ | ২ |
| ৩৯ | ইট্রিয়াম | ২, ৮, ১৮, ৯, ২ | ৩ |
| ৪০ | জিরকোনিয়াম | ২, ৮, ১৮, ১০, ২ | ৪ |
| ৪১ | নাইওবিয়াম | ২, ৮, ১৮, ১২, ১ | ৫ |
| ৪২ | মলিবডেনাম | ২, ৮, ১৮, ১৩, ১ | ৬ |
| ৪৩ | টেকনেশিয়াম | ২, ৮, ১৮, ১৩, ২ | ৭ |
| ৪৪ | রুথিনিয়াম | ২, ৮, ১৮, ১৫, ১ | ৮ |
| ৪৫ | রোডিয়াম | ২, ৮, ১৮, ১৬, ১ | ৯ |
| ৪৬ | প্যালেডিয়াম | ২, ৮, ১৮, ১৮ | ১০ |
| ৪৭ | সিলভার | ২, ৮, ১৮, ১৮, ১ | ১১ |
| ৪৮ | ক্যাডমিয়াম | ২, ৮, ১৮, ১৮, ২ | ১২ |
| ৪৯ | ইন্ডিয়াম | ২, ৮, ১৮, ১৮, ৩ | ১৩ |
| ৫০ | টিন | ২, ৮, ১৮, ১৮, ৪ | ১৪ |
| ৫১ | অ্যান্টিমনি | ২, ৮, ১৮, ১৮, ৫ | ১৫ |
| ৫২ | টেলুরিয়াম | ২, ৮, ১৮, ১৮, ৬ | ১৬ |
| ৫৩ | আয়োডিন | ২, ৮, ১৮, ১৮, ৭ | ১৭ |
| ৫৪ | জেনন | ২, ৮, ১৮, ১৮, ৮ | ১৮ |
| ৫৫ | সিজিয়াম | ২, ৮, ১৮, ১৮, ৮, ১ | ১ |
| ৫৬ | বেরিয়াম | ২, ৮, ১৮, ১৮, ৮, ২ | ২ |
| ৫৭ | ল্যান্থানাম | ২, ৮, ১৮, ১৮, ৯, ২ | |
| ৫৮ | সিরিয়াম | ২, ৮, ১৮, ১৯, ৯, ২ | |
| ৫৯ | প্রাসিওডিমিয়াম | ২, ৮, ১৮, ২১, ৮, ২ | |
| ৬০ | নিওডিমিয়াম | ২, ৮, ১৮, ২২, ৮, ২ | |
| ৬১ | প্রমিথিয়াম | ২, ৮, ১৮, ২৩, ৮, ২ | |
| ৬২ | সামেরিয়াম | ২, ৮, ১৮, ২৪, ৮, ২ | |
| ৬৩ | ইউরোপিয়াম | ২, ৮, ১৮, ২৫, ৮, ২ | |
| ৬৪ | গ্যাডালিনিয়াম | ২, ৮, ১৮, ২৫, ৯, ২ | |
| ৬৫ | টারবিয়াম | ২, ৮, ১৮, ২৭, ৮, ২ | |
| ৬৬ | ডিসপ্রোসিয়াম | ২, ৮, ১৮, ২৮, ৮, ২ | |
| ৬৭ | হোলমিয়াম | ২, ৮, ১৮, ২৯, ৮, ২ | |
| ৬৮ | আরবিয়াম | ২, ৮, ১৮, ৩০, ৮, ২ | |
| ৬৯ | থুলিয়াম | ২, ৮, ১৮, ৩১, ৮, ২ | |
| ৭০ | ইটারবিয়াম | ২, ৮, ১৮, ৩২, ৮, ২ | |
| ৭১ | লুটিশিয়াম | ২, ৮, ১৮, ৩২, ৯, ২ | ৩ |
| ৭২ | হ্যাফনিয়াম | ২, ৮, ১৮, ৩২, ১০, ২ | ৪ |
| ৭৩ | ট্যানটালাম | ২, ৮, ১৮, ৩২, ১১, ২ | ৫ |
| ৭৪ | টাংস্টেন | ২, ৮, ১৮, ৩২, ১২, ২ | ৬ |
| ৭৫ | রিনিয়াম | ২, ৮, ১৮, ৩২, ১৩, ২ | ৭ |
| ৭৬ | অসমিয়াম | ২, ৮, ১৮, ৩২, ১৪, ২ | ৮ |
| ৭৭ | ইরিডিয়াম | ২, ৮, ১৮, ৩২, ১৫, ২ | ৯ |
| ৭৮ | প্লাটিনাম | ২, ৮, ১৮, ৩২, ১৭, ১ | ১০ |
| ৭৯ | সোনা | ২, ৮, ১৮, ৩২, ১৮, ১ | ১১ |
| ৮০ | পারদ | ২, ৮, ১৮, ৩২, ১৮, ২ | ১২ |
| ৮১ | থ্যালিয়াম | ২, ৮, ১৮, ৩২, ১৮, ৩ | ১৩ |
| ৮২ | সীসা | ২, ৮, ১৮, ৩২, ১৮, ৪ | ১৪ |
| ৮৩ | বিসমাথ | ২, ৮, ১৮, ৩২, ১৮, ৫ | ১৫ |
| ৮৪ | পোলোনিয়াম | ২, ৮, ১৮, ৩২, ১৮, ৬ | ১৬ |
| ৮৫ | অ্যাস্টাটিন | ২, ৮, ১৮, ৩২, ১৮, ৭ | ১৭ |
| ৮৬ | রেডন | ২, ৮, ১৮, ৩২, ১৮, ৮ | ১৮ |
| ৮৭ | ফ্রান্সিয়াম | ২, ৮, ১৮, ৩২, ১৮, ৮, ১ | ১ |
| ৮৮ | রেডিয়াম | ২, ৮, ১৮, ৩২, ১৮, ৮, ২ | ২ |
| ৮৯ | অ্যাক্টিনিয়াম | ২, ৮, ১৮, ৩২, ১৮, ৯, ২ | |
| ৯০ | থোরিয়াম | ২, ৮, ১৮, ৩২, ১৮, ১০, ২ | |
| ৯১ | প্রোটেক্টিনিয়াম | ২, ৮, ১৮, ৩২, ২০, ৯, ২ | |
| ৯২ | ইউরেনিয়াম | ২, ৮, ১৮, ৩২, ২১, ৯, ২ | |
| ৯৩ | নেপচুনিয়াম | ২, ৮, ১৮, ৩২, ২২, ৯, ২ | |
| ৯৪ | প্লুটোনিয়াম | ২, ৮, ১৮, ৩২, ২৪, ৮, ২ | |
| ৯৫ | আমেরিসিয়াম | ২, ৮, ১৮, ৩২, ২৫, ৮, ২ | |
| ৯৬ | কুরিয়াম | ২, ৮, ১৮, ৩২, ২৫, ৯, ২ | |
| ৯৭ | বার্কিলিয়াম | ২, ৮, ১৮, ৩২, ২৭, ৮, ২ | |
| ৯৮ | ক্যালিফোর্নিয়াম | ২, ৮, ১৮, ৩২, ২৮, ৮, ২ | |
| ৯৯ | আইনস্টাইনিয়াম | ২, ৮, ১৮, ৩২, ২৯, ৮, ২ | |
| ১০০ | ফার্মিয়াম | ২, ৮, ১৮, ৩২, ৩০, ৮, ২ | |
| ১০১ | মেন্ডেলেভিয়াম | ২, ৮, ১৮, ৩২, ৩১, ৮, ২ | |
| ১০২ | নোবেলিয়াম | ২, ৮, ১৮, ৩২, ৩২, ৮, ২ | |
| ১০৩ | লরেনসিয়াম | ২, ৮, ১৮, ৩২, ৩২, ৮, ৩ (?) | ৩ |
| ১০৪ | রাদারফোর্ডিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১০, ২ | ৪ |
| ১০৫ | ডুবনিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১১, ২ | ৫ |
| ১০৬ | সিবর্গিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১২, ২ | ৬ |
| ১০৭ | বোহরিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৩, ২ | ৭ |
| ১০৮ | হ্যাসিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৪, ২ | ৮ |
| ১০৯ | মাইটনেরিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৫, ২ | ৯ |
| ১১০ | ডার্মস্টাটিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৭, ১ | ১০ |
| ১১১ | রন্টজেনিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৮, ১ | ১১ |
| ১১২ | কোপার্নিসিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৮, ২ | ১২ |
| ১১৩ | নিহোনিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৮, ৩ | ১৩ |
| ১১৪ | ফ্লেরোভিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৮, ৪ | ১৪ |
| ১১৫ | মস্কোভিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৮, ৫ | ১৫ |
| ১১৬ | লিভারমোরিয়াম | ২, ৮, ১৮, ৩২, ৩২, ১৮, ৬ | ১৬ |
| ১১৭ | টেনেসাইন | ২, ৮, ১৮, ৩২, ৩২, ১৮, ৭ (?) | ১৭ |
| ১১৮ | ওগানেসন | ২, ৮, ১৮, ৩২, ৩২, ১৮, ৮ | ১৮ |