অপেক্ষক (গণিত)
ফাংশন (ইংরেজি: function, প্রতিবর্ণীকৃত: ফ়াঙ্ক্শ্যন্) বা অপেক্ষক একটি গাণিতিক ধারণা যা দুইটি রাশির মধ্যে পারস্পরিক নির্ভরশীলতা প্রকাশ করে। একটি রাশিকে বলা হয় প্রদত্ত রাশি, বা স্বাধীন চলক বা ফাংশনটির আর্গুমেন্ট বা ইনপুট। অপরটিকে উৎপাদিত রাশি বা ফাংশনের মান বা আউটপুট বলা হয়। ফাংশন কোন একটি নির্দিষ্ট সেট থেকে (যেমন-বাস্তব সংখ্যার সেট থেকে) নেয়া প্রতিটি ইনপুট উপাদানের জন্য একটি অনন্য আউটপুটকে সম্পর্কিত করে। ফাংশনে সাধারনত f, g, F, G ইত্যাদি প্রতীক বা চিহ্ন দ্বারা প্রকাশ করা হয়।

কোনো ফাংশনকে বিভিন্ন উপায়ে প্রকাশ করা যায়: সূত্রের সাহায্যে, লেখচিত্রের সাহায্যে, ফাংশনটি গণনাকারী অ্যালগোরিদমের সাহায্যে, কিংবা ফাংশনটির বৈশিষ্ট্য বর্ণনা করে। কখনো কখনো একটি ফাংশনকে অন্য এক বা একাধিক ফাংশনের সাথে এর সম্পর্কের মাধ্যমে প্রকাশ করা হয় (যেমন- বিপরীত ফাংশন)। বিভিন্ন ব্যবহারিক শাস্ত্রে ফাংশনগুলিকে প্রায়শই তাদের মানের সারণি কিংবা সূত্রের মাধ্যমে প্রকাশ করা হয়। তবে সব ফাংশনকে উপরের সব রকমভাবে প্রকাশ করা যায় না। আসল ফাংশন ও একে কীভাবে উপস্থাপন করা হয়েছে বা কল্পনা করা হয়েছে, এ দুইয়ের মধ্যে যথেষ্ট পার্থক্য আছে। [তথ্যসূত্র প্রয়োজন]
কতিপয় গুরুত্বপূর্ণ সংজ্ঞা
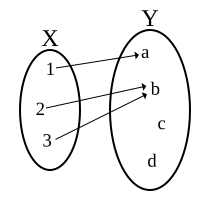
সম্পাদনাযদি X ও Y দুইটি সেট হয় এবং কোন নিয়মের অধীনে X সেটের প্রত্যেক উপাদানের সাথে Y সেটের একটি ও কেবল একটি উপাদানকে সংশ্লিষ্ট করা হয় তাহলে ঐ নিয়মকে X থেকে Y এ বর্ণিত একটি ফাংশন বা ফাংশান বলা হয়। এক্ষেত্রে X সেটকে বলা হয় ফাংশনটির ডোমেইন (গণিত) এবং Y সেটকে বলা হয় ফাংশনটির কোডমেইন । ডোমেইন হচ্ছে মুলত কোন ফাংশনকে সংজ্ঞায়িত করতে পারে এমন উপাদান নিয়ে গঠিত সেট। আবার, যদি f : X → Y ফাংশনের অধীনে x ∈ X এর সাথে y ∈ Y সংশ্লিষ্ট হয়, তাহলে উক্ত ফাংশনের অধীনে y-কে x-এর প্রতিবিম্ব বা ইমেজ বলা হয়, আর x-কে y-এর প্রাক-প্রতিবিম্ব বলা হয় এবং y=f(x) লিখে তা প্রকাশ করা হয়। এখানে, x-এর যে যে মানের জন্য ফাংশনটি সংজ্ঞায়িত হয় তাদেরকেই সাধারান ভাষায় ফাংশনের ডোমেইন আর y-এর মানগুলোকে ফাংশনের রেঞ্জ বলে।
ফাংশনের সংযোজন
সম্পাদনাফাংশনের সংযোজন (কমপজিশন) সমগ্র গণিতশাস্ত্রের অন্যতম গুরুত্বপূর্ণ একটি ধারণা: যদি z, y এর একটি ফাংশন হয়, যেখানে y, x-এর একটি ফাংশন, তবে z, x-এরও একটি ফাংশন হবে। সাধারণভাবে বলা যায় যে, যে সংযুক্ত ফাংশনটি প্রথম ফাংশনের আউটপুটকে দ্বিতীয় ফাংশনের ইনপুট হিসেবে ব্যবহার করে পাওয়া যায়। ফাংশনের এই বৈশিষ্ট্যটি অন্যান্য গাণিতিক সংগঠন (যেমন-সংখ্যা বা আকৃতি) থেকে ফাংশনকে স্বতন্ত্র করেছে এবং ফাংশনসমূহের তত্ত্বকে একটি শক্তিশালী কাঠামো প্রদান করেছে।
পরিভাষা ও উদাহরণ
সম্পাদনাগণিতে ফাংশন একটি মৌলিক ভূমিকা পালন করে। গণিতের বিমূর্ত শাখা যেমন সেট তত্ত্বে সাধারণ প্রকৃতির ফাংশন নিয়ে আলোচনা করা হয়। এই পদ্ধতিগুলো দৃঢ় নিয়মের উপর প্রতিষ্ঠিত নয় এবং পরিচিত নীতি দ্বারা পরিচালিত নয়। সর্বাধিক বিমূর্ত ক্ষেত্রে ফাংশনের পরিচিত বৈশিষ্ট্য হল এটি একটি ইনপুটের জন্য কেবল একটি আউটপুট দেয়। এমন ফাংশনের জন্য সংখ্যার প্রয়োজন হয় না এবং কোন শব্দের প্রথম অক্ষরও এক্ষেত্রে গ্রহণীয় হতে পারে। বীজগাণিতিক অপারেশনের পরিভাষার মাধ্যমে বীজগণিতে ব্যবহৃত ফাংশনের ব্যাখ্যা দেয়া সম্ভব।
বিভিন্ন প্রকার ফাংশনের নাম:
১. সার্বিক ফাংশন ২. এক-এক ফাংশন ৩. সার্বিক ও এক-এক ফাংশন ৪. বিপরীত ফাংশন ৫. অভেদ ফাংশন ৬. ধ্রুবক ফাংশন ৭. সংযোজিত ফাংশন ৮. বহুপদী ফাংশন ৯. মূলদীয় ফাংশন ১০. যোগাশ্রয়ী ফাংশন ১১. দ্বিঘাত ফাংশন ১২. ত্রিকোণমিতিক ফাংশন ১৩. পর্যাবৃত্ত ফাংশন ১৪. বৃত্তীয় ফাংশন ১৫. বিপরীত বৃত্তীয় ফাংশন ১৬. যুগ্ম ফাংশন ১৭. অযুগ্ম ফাংশন ১৮. সূচকীয় ফাংশন ১৯. লগারিদমিক ফাংশন
![{\displaystyle {\begin{aligned}&\scriptstyle f\colon [-1,1.5]\to [-1,1.5]\\&\textstyle x\mapsto {\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367545798d4c1d7748410deb9d03ea9faf400d6d)