ভূমি (জ্যামিতি)
কোন বহুভুজের যেকোন বাহুকে অথবা কোন বহুতলকের যেকোন তলকে, বিশেষ করে কোন জ্যামিতিক কাঠামোর যে দিক বরাবর উচ্চতা পরিমাপ করা হয় তার লম্বদিকে যা থাকে অথবা কাঠামোটির তলদেশে যে জিনিসটি অবস্থান করার কথা চিন্তা করা যায় জ্যামিতির ভাষায় তাকে ভূমি বা ভিত্তি বলা হয়। সাধারণত ত্রিভুজ, সামান্তরিক, ট্রাপিজিয়াম, সিলিন্ডার, শঙ্কু, পিরামিড, সামান্তরিকীয় বহুতলক এবং ফ্রাস্টামের ক্ষেত্রে এই শব্দটি প্রয়োগ করা হয়।[১] দ্বিমাত্রিক কাঠামোর ক্ষেত্রে অর্থাৎ বহুভুজের ক্ষেত্রে ভূমি বলতে বহুভুজটির কোন বাহুকে এবং বহুতলকের মতো ত্রিমাত্রিক কাঠামোর ক্ষেত্রে ভূমি বলতে এর কোন এক তলকে বোঝানো হয়।
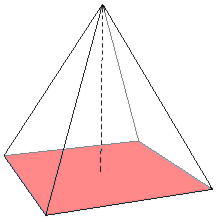
ক্ষেত্রফল ও আয়তন নির্ণয়ে ভূমির ব্যবহার
সম্পাদনামূলত জ্যামিতিক কাঠামোর ক্ষেত্রফল এবং আয়তন নির্ণয়ে উচ্চতার পাশাপাশি ভূমির ব্যবহার করা হয়। এক্ষেত্রে কোন কাঠামোর ভূমির পরিমাপকেই (নির্ণীত দৈর্ঘ্য বা ক্ষেত্রফলকে) কাঠামোটির ভূমিরূপে নির্দেশ করা হয়ে থাকে।
উচ্চতাকে ভূমির দ্বারা গুণ করে সামান্তরিকের ক্ষেত্রফল অথবা প্রিজম ও সিলিন্ডারের আয়তন পরিমাপ করা যেতে পারে। আবার, ত্রিভুজের ক্ষেত্রফল এবং শঙ্কু ও পিরামিডের আয়তন এই গুণফলের একেবারে সমান না হয়ে এর একটি ভগ্নাংশ হয়ে থাকে। এছাড়া ট্রাপিজিয়াম এবং ফ্রাস্টামের মতো কিছু কাঠামোতে দুটি সমান্তরাল ভূমিও থাকে যাদের উভয়কেই কাঠমোটির দ্বারা আবদ্ধ এলাকার পরিমাণে ব্যবহার করা হয়।[২]
ত্রিকোণমিতিতে বর্ধিত বাহুর প্রয়োগ
সম্পাদনাকোন বহুভুজের যে বাহুকে ভূমি ধরা হয় তাকে একটি নির্দিষ্ট বিন্দু পর্যন্ত বর্ধিত করলে যে রেখা পাওয়া যায় তাই বর্ধিত ভূমি। অর্থাৎ, কোন বহুভুজের বর্ধিত ভূমি হল রেখার বর্ধিতাংশবিশেষ যার মধ্যে বহুভুজটির ভূমি অন্তর্ভুক্ত থাকে। স্থুলকোণী ত্রিভুজের ক্ষেত্রে বর্ধিত ভূমি গুরুত্বপূর্ণ। স্থুলকোণী ত্রিভুজের কোন সূক্ষ্ম কোণ থেকে অঙ্কিত উচ্চতা বা উচ্চতারেখা ত্রিভুজটির বাইরে অবস্থান করে এবং এই উচ্চতারেখা সূক্ষ্ম কোণটির বিপরীতে থাকা বাহুর বর্ধিত অংশকে অর্থাৎ বর্ধিত ভূমিকে যা প্রকৃতপক্ষে ভূমি নয় তাকে লম্বভাবে ছেদ ছেদ করে।
তথ্যসূত্র
সম্পাদনা- ↑ Palmer, C.I.; Taylor, D.P. (১৯১৮)। Plane Geometry। Scott, Foresman & Co.। পৃষ্ঠা 38, 315, 353।
- ↑ Jacobs, Harold R. (২০০৩)। Geometry: Seeing, Doing, Understanding (Third সংস্করণ)। New York City: W. H. Freeman and Company। পৃষ্ঠা 281। আইএসবিএন 978-0-7167-4361-3।