অমূলদ সংখ্যা

অমূলদ সংখ্যা হল সেসব বাস্তব সংখ্যা যেগুলোকে দুটি পূর্ণ সংখ্যার অনুপাতে প্রকাশ করা যায় না। অমূলদ সংখ্যাকে দশমিক-এ প্রকাশ করার চেষ্টা করলে দশমিকের পর যত ঘর অবধি-ই দেখা হবে, কোন পৌনঃপুনিকতা (recurrence) দেখা যাবে না।

π

হচ্ছে সবচেয়ে বেশি পরিচিত অমূলদ সংখ্যা।

{\sqrt {2}}

এর মান একটি অমূলদ সংখ্যা।

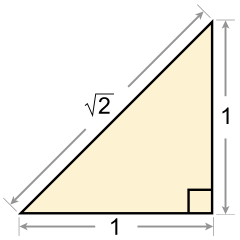
অমূলদ সংখ্যার মধ্যে বৃত্তের পরিধি ও ব্যাসের অনুপাত π, ইউলারের সংখ্যা e, গোল্ডেন অনুপাত φ এবং দুটি এর বর্গমূল ${\sqrt {2}}$ ;^[১]^[২]^[৩] আসলে বর্গসংখ্যা বাদে সকল অখণ্ডসংখ্যার সমস্ত বর্গমূল, অমূলদ।

ইতিহাসসম্পাদনা

প্রাচীন গ্রিসে পিথাগোরাস সম্পর্কিত অমুলদ সংখার ইতিহাসটি বেশ রোমাঞ্চকর। হিপ্পসাস নামক পিথাগোরাসের শিষ্য( যারা পিথাগোরিয়ান নামে পরিচিত) ${\sqrt {2}}$ আবিস্কার করেন। হিপ্পসাস পিথাগোরাসের সদ্য আবিস্কৃত সমকোণী ত্রিভুজের সূত্র (কোন সমকোনী ত্রিভূজের অতিভূজের উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বৰ্গক্ষেত্রেরদ্বয়ের সমষ্টির সমান)ব্যবহার করে, দুই বাহুর দৈর্ঘ্য ১ একক ধরে, অতিভুজ বের করতে গিয়ে একটা গোল বাধিয়ে ফেলেন। তিনি কিছুতেই অতিভুজ হিসাবে যে ${\sqrt {2}}$ পেয়েছেন তার মান আর হিসাব করতে পারছিলেন না। পরে বুঝলেন যে, এটা আর সব অন্য মুলদ সংখ্যার মত নয়, যাদের দুইটি পুর্ণ সংখ্যার অনুপাত আকারে লেখা সম্ভব। পরবর্তিতে আরো এরকম সংখ্যা আবিস্কৃত হয়। আর গণিতবিদেরা এদের নাম দেন অমুলদ সংখ্যা। প্রাচীন ভারতবৰ্ষেও অমূলদ সংখ্যার চিহ্ন পাওয়া যায়৷ শ্রীনিবাস রামানুজন বলেছিলেন যে ${\sqrt {2}}$ এর মান যতো খুশি ততো ঘর। অতি সুপরিচিত একটি অমুলদ সংখ্যা হচ্ছে বৃত্তের পরিধি ও ব্যাসের অনুপাত(যাকে গ্রিক অক্ষর পাই π দ্বারা নির্দেশ করা হয়)। π= ৩.১৪১৫৯২৬৫ .......

প্রকারভেদসম্পাদনা

তুরীয় সংখ্যা (ইংরেজীতে transcendental number )
বীজগাণিতিক সংখ্যা (ইংরেজীতে algebraic tamim

তথ্যসূত্রসম্পাদনা

↑ http://www.mathsisfun.com/irrational-numbers.html; URL retrieved 24 October 2007.
↑ ওয়েস্টিন, এরিক ডব্লিউ., গণিত বিশ্ব থেকে "Irrational Number"। URL retrieved 26 October 2007.
↑ The 15 Most Famous Transcendental Numbers. by Clifford A. Pickover. URL retrieved 24 October 2007.

আরো পড়াসম্পাদনা

Adrien-Marie Legendre, Éléments de Géometrie, Note IV, (1802), Paris
Rolf Wallisser, "On Lambert's proof of the irrationality of π", in Algebraic Number Theory and Diophantine Analysis, Franz Halter-Koch and Robert F. Tichy, (2000), Walter de Gruyer

বহিঃসংযোগসম্পাদনা

Zeno's Paradoxes and Incommensurability (n.d.). Retrieved April 1, 2008
ওয়েস্টিন, এরিক ডব্লিউ., গণিত বিশ্ব থেকে "Irrational Number"।

[1] ttp://www.mathsisfun.com/irrational-numbers.html; URL retrieved 24 October 2007.

[2] ওয়েস্টিন, এরিক ডব্লিউ., গণিত বিশ্ব থেকে "Irrational Number"। URL retrieved 26 October 2007.

[3] The 15 Most Famous Transcendental Numbers. by Clifford A. Pickover. URL retrieved 24 October 2007.

[১]

[২]

[৩]