অভেদ

কয়েকটি চলকের সমন্বয়ে গঠিত হয় বা হতে পারে এমন দুটি গাণিতিক রাশিমালা A এবং B-এর সম্পর্কের ক্ষেত্রে অভেদ হলো ঐ রাশিমালা দুটির একটির সাথে অপরটির সম্পর্কজনিত এমন একটি সমতা, যেখানে একটি নির্দিষ্ট বৈধ সীমার মধ্যে চলকের সকল বা যেকোনো মানের জন্য A এবং B উভয়ই একই মান প্রদান করে। অন্যভাবে বলা যায়, A = B একটি অভেদ হবে যদি A এবং B একই ফাংশনকে সংজ্ঞায়িত করে। উপরন্তু, অভেদ হলো পৃথক পৃথকভাবে সংজ্ঞায়িত দুটি ফাংশনের মধ্যকার একটি সমতা। উদাহরণস্বরূপ, $(a+b)^{2}=a^{2}+2ab+b^{2}$ এবং $\cos ^{2}\theta +\sin ^{2}\theta =1$ হচ্ছে অভেদ। অভেদ আদতে এক প্রকার সমীকরণ যাকে বিশেষ কিছু শর্ত মেনে চলতে হয়। অভেদকে সচরাচর সমান চিহ্ন = দিয়ে নির্দেশ করা হয়। তবে কখনো কখনো তৎপরিবর্তে তিনটি অনুভূমিক রেখা তথা ত্রিঘাই ≡ ব্যবহার করা হয়।

যেকোনো কোণ $\theta$ ও একক বৃত্তের ওপর অবস্থিত বিন্দু $(x,y)=(\cos \theta ,\sin \theta )$ এর জন্য পিথাগোরাসীয় অভেদ $\cos ^{2}\theta +\sin ^{2}\theta =1$ এর দৃশ্যমান প্রমাণ। এই অভেদটি $x^{2}+y^{2}=1$ সমীকরণকে মেনে চলে।

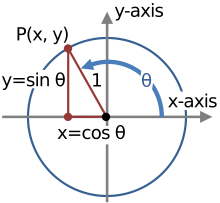
সাধারণ কিছু অভেদ

বীজগাণিতিক অভেদ

আরও দেখুন: উৎপাদকে বিশ্লেষণ

$a+0=a$ ও $a+(-a)=0$ এর মতো নির্দিষ্ট অভেদসমূহ বীজগণিতের ভিত্তি গঠন করেছে। আবার $(a+b)^{2}=a^{2}+2ab+b^{2}$ এবং $a^{2}-b^{2}=(a+b)(a-b)$ এর মতো অন্যান্য বীজগাণিতিক অভেদসমূহ বীজগাণিতিক রাশিমালাসমূহের সরলীকরণে এবং সেগুলোর সম্প্রসারণে সুবিধাজনক ভুমিকা পালন করতে পারে।

কম্বিনাটোরিয়াল অভেদ

মূল নিবন্ধ: কম্বিনাটোরিয়াল অভেদসমূহের তালিকা

কম্বিনাটরিক্স এর মূল বিষয় গোনা বা কাউন্ট করা। এখানে কিছু গুরুত্বপূর্ণ কম্বিনাটোরিয়াল অভেদ দেওয়া হলো, যা বীজগাণিতিক ভাবে বা কম্বিনাটোরিয়াল যুক্তি দুটো দিয়েই প্রমাণ করা যায়

১. ধনাত্মক বাস্তব অখন্ড ঘাতের জন্য দ্বিপদ উপপাদ্য:-

$$(x+y)^{n}={n \choose 0}x^{n}y^{0}+{n \choose 1}x^{n-1}y^{1}+{n \choose 2}x^{n-2}y^{2}+\cdots +{n \choose n-1}x^{1}y^{n-1}+{n \choose n}x^{0}y^{n},$$

যেখানে $n\geq 0$ একটি পূর্ণ সংখ্যা এবং প্রতিটি ${\tbinom {n}{k}}$ একটি করে পূর্ণসংখ্যা যা দ্বিপদ সহগ নামে পরিচিত। সমষ্টি চিহ্ন ব্যবহার করে এটিকে লেখা যায় যে

$$(x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}y^{k}=\sum _{k=0}^{n}{n \choose k}x^{k}y^{n-k}.$$

২. ধনাত্মক বাস্তব অখন্ড ঘাতের জন্য দ্বিপদ উপপাদ্য:-

যখন | x | >| y |. আর r একটি জটিল সংখ্যা,

$${\begin{aligned}(x+y)^{r}&=\sum _{k=0}^{\infty }{r \choose k}x^{r-k}y^{k}\\&=x^{r}+rx^{r-1}y+{\frac {r(r-1)}{2!}}x^{r-2}y^{2}+{\frac {r(r-1)(r-2)}{3!}}x^{r-3}y^{3}+\cdots .\end{aligned}}$$

৩. ভ্যান্ডারমোন্ডের অভেদ

${m+n \choose r}=\sum _{k=0}^{r}{m \choose k}{n \choose r-k}$

যেকোনো অঋণাত্মক পূর্ণসংখ্যা r, m, n. এর জন্য।

৪. পাস্কালের অভেদ ${n-1 \choose k}+{n-1 \choose k-1}={n \choose k},$ যখন n and k ধনাত্মক পূর্ণসংখ্যা।

ত্রিকোণমিতিক অভেদ

মূল নিবন্ধ: ত্রিকোণমিতিক অভেদসমূহের তালিকা

জ্যামিতিকভাবে ত্রিকোণমিতিক অভেদ হচ্ছে সেসব অভেদ যে অভেদসমূহ এক বা একাধিক কোণের নির্দিষ্ট ফাংশনের সাথে সম্পর্কিত। অপরদিকে ত্রিভুজীয় অভেদসমূহ ত্রিভুজের কোণ ও বাহু উভয়েরই সাথে জড়িত। ত্রিকোণমিতিক অভেদসমূহ ত্রিভুজীয় অভেদসমূহের থেকে স্বতন্ত্র। এই অনুচ্ছেদে কেবল ত্রিকোণমিতিক অভেদগুলোই আলোচনা করা হয়েছে।

ত্রিকোণমিতিক ফাংশন সম্পর্কিত রাশিমালাগুলোর সরলীকরণের প্রয়োজন পড়লে এই অভেদগুলো সর্বদা সহায়ক ভূমিকা পালন করে। এই অভেদগুলোর আরেকটি গুরুত্বপূর্ণ প্রয়োগ হচ্ছে, ত্রিকোণমিতিক নয় এমন ফাংশনসমূহের সমাকলন, যা এমনই এক সাধারণ কৌশল যেখানে প্রথমতঃ একটি ত্রিকোণমিতিক ফাংশনযুক্ত প্রতিস্থাপন-সূত্রের প্রয়োগ করা হয়, এবং শেষে একটি ত্রিকোণমিতিক অভেদ দিয়ে ফলাফল প্রদানকারী যোগজটিকে সরলীকরণ করা হয়।

সবচেয়ে বেশি উল্লেখ করার মতো ত্রিকোণমিতিক অভেদের উদাহরণগুলোর মধ্যে একটি $\sin ^{2}\theta +\cos ^{2}\theta =1$ সমীকরণটির সাথে সম্পর্কিত, যেখানে এই সমীকরণটি $\theta$-এর সকল বাস্তব মানের জন্য সত্য। পক্ষান্তরে, নিচের সমীকরণটি দেখা যাক:

$\cos \theta =1$

এই সমীকরণটি $\theta$-এর কেবল নির্দিষ্ট মানগুলোর জন্যই সত্য, সকল মানের জন্য সত্য নয়। উদাহরণস্বরূপ, এই সমীকরণটি তখনই সত্য হবে যদি $\theta =0$ হয়। কিন্তু $\theta =2$ হলে সমীকরণটি মিথ্যা হবে।

অন্য আরেক প্রকার ত্রিকোমিতিক অভেদ রয়েছে যেগুলো তথাকথিত ত্রিকোণমিতিক যোগ-বিয়োগ সংশ্লিষ্ট। বড় কোণযুক্ত রাশিমালাগুলোকে ছোট কোণযুক্ত রাশিমালায় ভাঙতে এধরনের অভেদগুলো প্রয়োগ করা যায়। দুটি কোণযুক্ত অভেদ $\sin(2\theta )=2\sin \theta \cos \theta$ এবং $\tan(x+y)$) এর যোগের সূত্র হলো এজাতীয় ত্রিকোমিতিক অভেদের নমুনা।

সূচকীয় অভেদ

মূল নিবন্ধ: সূচকীকরণ

ভিত্তি শূন্য নয় এই শর্তে নিচের অভেদগুলো যেকোনো পূর্ণ সংখ্যার সূচকের জন্য সত্য:

${\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}$

যোগ ও গুণের ক্ষেত্রে বিনিময় বিধি কাজ করলেও সূচকের ক্ষেত্রে তা কাজ করে না, অর্থাৎ সূচকীকরণ বিনিময়ধর্মী নয়। যেমন: যোগ ও গুণের বেলায় 2 + 3 = 3 + 2 = 5 এবং 2 · 3 = 3 · 2 = 6, কিন্তু সূচকের ক্ষেত্রে 2³ = 8 যেখানে 3² = 9।

এছাড়াও, সূচকীকরণ সংযোগ বিধিও মেনে চলে না, যোগ ও গুণের ক্ষেত্রে যা কার্যকর। যেমন: যোগ ও গুণের বেলায় (2 + 3) + 4 = 2 + (3 + 4) = 9 এবং (2 · 3) · 4 = 2 · (3 · 4) = 24, কিন্তু সূচকের ক্ষেত্রে 2³ to the 4 অর্থাৎ 2³-এর উপর 4 ঘাত হবে 8⁴ (বা, 4,096); যেখানে, 2 to the 3⁴ অর্থাৎ 2-এর উপর 3⁴ নিলে পাওয়া যাবে 2⁸¹ (বা 2,417,851,639,229,258,349,412,352)। বন্ধনী না লিখলে এবং রীতি অনুসারে উপর থেকে নিচের দিকে অর্থাৎ ঘাত থেকে ভিত্তির দিকের ক্রমানুসরণ করা হলে এদেরকে নিম্নরূপে পাওয়া যাবে:

$b^{p^{q}}:=b^{(p^{q})},$   যেখানে   $(b^{p})^{q}=b^{p\cdot q}.$

লগারিদমিক অভেদ

মূল নিবন্ধ: লগারিদমিক অভেদসমূহের তালিকা

লগারিদমিক অভেদ বা লগের সূত্র নামে পরিচিত বেশ কিছু গুরুত্বপূর্ণ সূত্র লগারিদমসমূহের পরস্পরের মধ্যে সম্পর্ক স্থাপন করে।

গুণফল, ভাগফল, ঘাত এবং মূল

কোনো গুণফলের লগারিদম ঐ গুণফলটি যে সংখ্যাগুলো থেকে এসেছে তাদের লগারিদমের সমষ্টির সমান এবং দুটি সংখ্যার অনুপাতের লগারিদম ঐ সংখ্যাদ্বয়ের লগারিদমের পার্থক্যের সমান। আবার, p-তম ঘাতযুক্ত কোনো সংখ্যার লগারিদম p এবং ঐ সংখ্যার লগারিদমের গুণফলের সমান। কোনো সংখ্যার p-তম মূলের লগারিদম ঐ সংখ্যার লগারিদমকে p দ্বারা ভাগ করে প্রাপ্ত সংখ্যার সমান। নিচের ছকে উদাহরণসহ এই অভেদগুলোর তালিকা দেওয়া হয়েছে। লগারিদমের সংজ্ঞা $x=b^{\log _{b}x},$ এবং/অথবা $y=b^{\log _{b}y}$ এর বামপক্ষে প্রতিস্থাপনের মাধ্যমে এই অভেদগুলোী প্রতিটিই প্রতিপাদন করা যায়।

	সূত্র	উদাহরণ
গুণফল	$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)$	$\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5$
ভাগফল	$\log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)$	$\log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4$
ঘাত	$\log _{b}(x^{p})=p\log _{b}(x)$	$\log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6$
মূল	$\log _{b}\!{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}$	$\log _{10}\!{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5$

ভিত্তির পরিবর্তন

log_b(x) লগারিদমটিকে একটি ইচ্ছামাফিক নির্ধারিত ভিত্তি k-এর সাপেক্ষে x এবং b-এর লগারিদম থেকে নিচের সূত্রের মাধ্যমে গণনা করা যায়:

$\log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.$

সাধারণ বৈজ্ঞানিক ক্যালকুলেটরগুলোতে মূলত ভিত্তি 10 এবং e-এর সাপেক্ষে লগারিদমের হিসাব করার সুযোগ থাকে। এহেন পরিস্থিতিতে, অন্য যেকোনো ভিত্তি b-এর সাপেক্ষে কোনো লগারিদম নির্ণয় করার ক্ষেত্রে, পূর্বোক্ত সূত্রে 10 ভিত্তিক এবং e ভিত্তিক এই লগারিদম দুটির যেকোনটি ব্যবহার করে গণনা করা যেতে পারে। এক্ষেত্রে সূত্রটি যেমনটা দেখাবে:

$\log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e}(x)}{\log _{e}(b)}}.$

একটি অজানা ভিত্তি b-এর সাপেক্ষ নির্দিষ্ট সংখ্যা x-এর লগারিদম log_b(x) এর ক্ষেত্রে এই ভিত্তিকে নিম্নোক্ত সূত্রের মাধ্যমে পাওয়া যাবে:

$b=x^{\frac {1}{\log _{b}(x)}}.$

অধিবৃত্তীয় ফাংশনের অভেদ

মূল নিবন্ধ: অধিবৃত্তীয় ফাংশন

অধিবৃত্তীয় ফাংশনসমূহ অনেক অভেদ মেনে চলে। গঠনগতভাবে এদের সবকটিই ত্রিকোণমিতিক অভেদগুলোর অনুরূপ। সত্য এই যে, অসবর্নের সূত্র দিয়ে নির্দিষ্ট কিছু শর্তের পূর্ণ প্রয়োগের মাধ্যমে যেকোনো ত্রিকোণমিতিক অভেদকে একটি অধিবৃত্তীয় অভেদে রূপান্তরিত করা যায়। এই সূত্রানুসারে, sine এবং cosine-এর পূর্ণসংখ্যার-ঘাতের পরিপ্রেক্ষিতে sine-কে sinh-এ এবং cosine-কে cosh-এ পরিবর্তন করে এবং জোড় সংখ্যক অধিবৃত্তীয় sine-সমূহের একটি গুণফল ধারণ করে এমন প্রতিটি পদের চিহ্ন পরিবর্তন করে যেকোনো ত্রিকোণমিতিক অভেদকে অধিবৃত্তীয় অভেদে রূপান্তর করা যায়।

গুডারম্যানীয় ফাংশন ত্রিকোণমিতিক ফাংশনসমূহের সাথে জটিল সংখ্যার সম্পৃক্ততামুক্ত এমন একটি অধিবৃত্তীয় ফাংশনের একটি সরাসরি সম্পর্ক প্রদান করে।

লজিক এবং সার্বজনীন বীজগণিত

পুস্তকি ভাষায় অভেদ হলো $\forall x_{1},\ldots ,x_{n}:s=t,$ আকারে গঠিত একটি সর্বজনীন সংখ্যায়িত প্রকৃত সূত্র, যেখানে, s এবং t হচ্ছে শর্ত যার $x_{1},\ldots ,x_{n}.$ ব্যতিত অন্য কোনো মুক্ত চলক নেই। যখন এই সূত্রটিকে একটি অভেদ হিসেবে বর্ণিত করা হয়, তখন $\forall x_{1},\ldots ,x_{n}$ কোয়ান্টিফায়ার উপসর্গটি সচরাচর বামপক্ষের ইমপ্লিসিট ফাংশন হয়। যেমন: কোনো মনোয়েডের স্বীকার্যকে সাধারণত নিচের সূত্রের আকারে লেখা হয়:

$\forall x,y,z:x*(y*z)=(x*y)*z,\quad \forall x:x*1=x,\quad \forall x:1*x=x,$

কিংবা সংক্ষেপে লেখা হলে এইভাবে:

$x*(y*z)=(x*y)*z,\qquad x*1=x,\qquad 1*x=x.$

তাই, এই সূত্রগুলো প্রতিটি মনোয়েডের ক্ষেত্রেই অভেদ। যেকোনো সমতার বেলায় কোয়ান্টিফায়ার বিহীন সূত্রগুলোকে বলা হয় সমীকরণ। আরেকভাবে বলা যায়, অভেদ হলো এমন একটি সমীকরণ যা চলকের সকল মানের জন্য সত্য।

তথসূত্র

উৎস

• Downing, Douglas (২০০৩)। Algebra the Easy Way। Barrons Educational Series। আইএসবিএন 978-0-7641-1972-9। উদ্ধৃতি টেমপ্লেট ইংরেজি প্যারামিটার ব্যবহার করেছে (link)
• Kate, S.K.; Bhapkar, H.R. (২০০৯)। Basics Of Mathematics। Technical Publications। আইএসবিএন 978-81-8431-755-8। উদ্ধৃতি টেমপ্লেট ইংরেজি প্যারামিটার ব্যবহার করেছে (link)
• Shirali, S. (২০০২)। Adventures in Problem Solving। Universities Press। আইএসবিএন 978-81-7371-413-9। উদ্ধৃতি টেমপ্লেট ইংরেজি প্যারামিটার ব্যবহার করেছে (link)

বহিঃসংযোগ

• The Encyclopedia of Equation Online encyclopedia of mathematical identities (archived)
• A Collection of Algebraic Identities