পরাক্ষ
জ্যামিতিতে, একটি উপবৃত্তের পরাক্ষ বা বৃহৎ অক্ষ হচ্ছে তার দীর্ঘতম ব্যাস । দীর্ঘতম ব্যাস হলো উপবৃত্তের সেই রেখাংশ যা উপবৃত্তের কেন্দ্র এবং উভয় ফোকাসের মধ্য দিয়ে যায় এবং যার প্রান্তীয় বিন্দুদ্বয় উপবৃত্তের পরিধির সবথেকে বিস্তৃত প্রান্তে গিয়ে শেষ হয়।
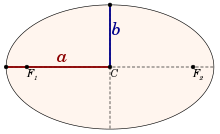
অর্ধ-বৃহৎ অক্ষ (আরও সঠিকভাবে, বৃহৎ অর্ধাক্ষ) হচ্ছে উপবৃত্তের বৃহৎ অক্ষের অর্ধেক যা এর কেন্দ্র থেকে শুরু হয়ে ফোকাসের মধ্য দিয়ে অতিক্রম করে পরিধিতে গিয়ে শেষ হয়। আর উপবৃত্ত বা অধিবৃত্তের অর্ধ-ক্ষুদ্র অক্ষ (আরও সঠিকভাবে, ক্ষুদ্র অর্ধাক্ষ) হচ্ছে এমন একটি রেখাংশ যা অর্ধ-বৃহৎ অক্ষের উপর লম্ব এবং যার একটি প্রান্ত কনিকের কেন্দ্রে অবস্থান করে। তবে বিশেষ ক্ষেত্রে যেমন একটি বৃত্তের জন্য, উভয় অর্ধাক্ষের দৈর্ঘ্যই বৃত্তের ব্যাসার্ধের সমান।
একটি উপবৃত্তের অর্ধ-বৃহৎ অক্ষের দৈর্ঘ্য a ও অর্ধ-ক্ষুদ্র অক্ষের দৈর্ঘ্য b এর মধ্যবর্তী সম্পর্ক, উৎকেন্দ্রিকতা e এবং অর্ধ-নাভিলম্ব এর সাহায্যে নিম্নরূপে বিবৃত করা যায়:
প্রচলিত রীতির উপর নির্ভর করে একটি অধিবৃত্তের অর্ধ-বৃহৎ অক্ষ হচ্ছে, দুটি শাখার মধ্যবর্তী দুরত্বের ধনাত্মক অথবা ঋণাত্মক মানের সমান। অর্থাৎ এটি হচ্ছে কেন্দ্র থেকে অধিবৃত্তের যেকোনো একটি শীর্ষবিন্দুর দুরত্বের সমান।
একটি পরাবৃত্তকে এমনভাবে উপবৃত্তের সীমার মধ্যে সংজ্ঞায়িত করা যায় যেখানে উপবৃত্তের একটি ফোকাস স্থির এবং অন্য ফোকাসটিকে একদিকে ইচ্ছামত সরিয়ে নেয়া যায়, যাতে স্থির থাকে। অর্থাৎ a এবং b অসীমতক হয়, তবে a, b এর চেয়ে দ্রুততর হবে।
বৃহৎ এবং ক্ষুদ্র অক্ষ এই বক্ররেখাগুলোর প্রতিসমতার অক্ষ: উপবৃত্তে ছোটটি ক্ষুদ্র অক্ষ; অধিবৃত্তের ক্ষুদ্র অক্ষ হচ্ছে যেটি অধিবৃত্তটিকে ছেদ করে না।
উপবৃত্ত
সম্পাদনাএকটি উপবৃত্তের সমীকরণ হচ্ছে:
যেখানে (h,k) কার্টেসিয় স্থানাঙ্ক ব্যবস্থায় উপবৃত্তের কেন্দ্র, এবং (x, y) উপবৃত্তের উপরিস্থিত যেকোনো বিন্দু।
অর্ধ-বৃহৎ অক্ষ হচ্ছে উপবৃত্তের ফোকাস থেকে পরিধির সর্বোচ্চ ও সর্বনিম্ন দূরত্ব ও এর গড় — যা, একটি ফোকাস থেকে বৃহৎ অক্ষের প্রান্তবিন্দুসমূহের দূরত্ব। জ্যোতির্বিদ্যায় এই সর্বোচ্চ দূরত্ব দুটিকে অপভূ বলা হয়।
উপবৃত্তের অর্ধ-ক্ষুদ্র অক্ষ হচ্ছে এই দূরত্বদ্বয়ের জ্যামিতিক গড়:
উপবৃত্তের উৎকেন্দ্রিকতা নিম্নরূপে সংজ্ঞায়িত করা হয়
- so .
এখন পোলার স্থানাঙ্কে এই সমীকরণটিকে বিবেচনা করি, যেখানে একটি ফোকাস মূলবিন্দুতে এবং অন্যটি অভিমুখে অবস্থিত,
ও এর জন্য ও এর গড় মান
উপবৃত্তে, the semi-major axis is the geometric mean of the distance from the center to either focus and the distance from the center to either directrix.
The semi-minor axis of an ellipse runs from the center of the ellipse (a point halfway between and on the line running between the foci) to the edge of the ellipse. The semi-minor axis is half of the minor axis. The minor axis is the longest line segment perpendicular to the major axis that connects two points on the ellipse's edge.
The semi-minor axis b is related to the semi-major axis a through the eccentricity e and the semi-latus rectum , as follows:
A parabola can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping fixed. Thus a and b tend to infinity, a faster than b.
The length of the semi-minor axis could also be found using the following formula,[১]
where f is the distance between the foci, p and q are the distances from each focus to any point in the ellipse.
অধিবৃত্ত
সম্পাদনাThe semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches; if this is a in the x-direction the equation is:
In terms of the semi-latus rectum and the eccentricity we have
The transverse axis of a hyperbola coincides with the major axis.[২]
In a hyperbola, a conjugate axis or minor axis of length , corresponding to the minor axis of an ellipse, can be drawn perpendicular to the transverse axis or major axis, the latter connecting the two vertices (turning points) of the hyperbola, with the two axes intersecting at the center of the hyperbola. The endpoints of the minor axis lie at the height of the asymptotes over/under the hyperbola's vertices. Either half of the minor axis is called the semi-minor axis, of length b. Denoting the semi-major axis length (distance from the center to a vertex) as a, the semi-minor and semi-major axes' lengths appear in the equation of the hyperbola relative to these axes as follows:
The semi-minor axis is also the distance from one of focuses of the hyperbola to an asymptote. Often called the impact parameter, this is important in physics and astronomy, and measure the distance a particle will miss the focus by if its journey is unperturbed by the body at the focus.
The semi-minor axis and the semi-major axis are related through the eccentricity, as follows:
উল্লেখ্য যে, অধিবৃত্তে b এর মান a এর চেয়ে বেশি হতে পারে। [১] ওয়েব্যাক মেশিনে আর্কাইভকৃত ২৪ অক্টোবর ২০১৮ তারিখে
জ্যোতির্বিদ্যা
সম্পাদনাকক্ষীয় পর্যায়কাল
সম্পাদনাগড় দূরত্ব
সম্পাদনাআরো দেখুন
সম্পাদনা- Semidiameter
তথ্যসূত্র
সম্পাদনা- ↑ http://www.mathopenref.com/ellipseaxes.html,"Major[স্থায়ীভাবে অকার্যকর সংযোগ] / Minor axis of an ellipse",Math Open Reference, 12 May 2013
- ↑ "7.1 Alternative Characterization"। www.geom.uiuc.edu। ২৪ অক্টোবর ২০১৮ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২৭ জুলাই ২০১৯।
- ↑ "The Geometry of Orbits: Ellipses, Parabolas, and Hyperbolas"। www.bogan.ca।

