ক্ষুদ্রবিবর
ক্ষুদ্রবিবর বা ওয়ার্মহোল যা আইনস্টাইন-রোজেন সেতু নামেও পরিচিত, হলো স্থান-কালের একটি টপোগণিতিক বৈশিষ্ট্য যা মৌলিকভাবে মহাবিশ্বের দুই প্রান্ত বা দুই মহাবিশ্বের মধ্যে স্থান-কালের ক্ষুদ্র সুড়ঙ্গপথ বা "শর্টকাট"। যদিও গবেষকরা এখনো ক্ষুদ্রবিবর পর্যবেক্ষণ করতে পারেননি তবে আইনস্টাইনের সাধারণ আপেক্ষিকতার সমীকরনে এর বৈধ সমাধান রয়েছে, কারণ এর তাত্ত্বিক শক্তি খুব জোরালো। সাধারণ আপেক্ষিকতা অধ্যাপনার জন্য ক্ষুদ্রবিবর হচ্ছে পদার্থবিদ্যার আদর্শ রুপক। শোয়ার্যসচাইল্ড ওয়ার্মহোল সমাধান হচ্ছে প্রথম টাইপ আবিষ্কৃত ক্ষুদ্রবিবর যার মুল ভিত্তি হল শোয়ার্যসচাইল্ড ম্যাট্রিক তত্ত্ব যা একটি অনন্ত কৃষ্ণ বিবর বর্ণনা করে, কিন্তু পরবর্তীতে দেখা যায় এই ধরনের ক্ষুদ্রবিবর কোন বস্তুর পারাপারের জন্য ততটা সময় সাপেক্ষ নয় কারণ এটি ক্ষণস্থায়ী।
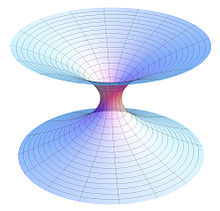
ক্ষুদ্রবিবর কল্পনা করার জন্য একটা দ্বিমাত্রিক তল, যেমন কাগজ তলের কথা ভাবুন। এর এক স্থানে রয়েছে একটি ছিদ্র যা থেকে একটি ত্রিমাত্রিক টিউব বা সুড়ঙ্গ বের হয়, এবং সেটি কাগজের অন্য একটি অংশে আরেকটি ছিদ্রে গিয়ে মিলিত হয়। দ্বিমাত্রিক কাগজের উপর দিয়ে দুটি ছিদ্রের দূরত্ব বেশি হলেও সুড়ঙ্গ দিয়ে দূরত্ব কম, কারণ এটি কাগজটিকে ত্রিমাত্রিকভাবে বাঁকিয়ে নিয়ে সুড়ঙ্গপথটির দৈর্ঘ্য কমিয়ে দিয়েছে। ওর্মহোলের ব্যাপারটাও অনেকটা এমন, যদিও এখানে দ্বিমাত্রিক কাগজ পৃষ্ঠের বদলে রয়েছে ত্রিমাত্রিক মহাকাশ, এবং ত্রিমাত্রিক সুড়ঙ্গের বদলে রয়েছে চতুর্মাত্রিক ওয়ার্মহোল। বিভিন্ন সাইন্স ফিকশন, উপন্যাস এ ক্ষুদ্রবিবরের অস্তিত্ব পাওয়া যায়।
ম্যাট্রিক
সম্পাদনাক্ষুদ্রবিবর ম্যাট্রিক তত্ত্ব একটি ক্ষুদ্রবিবরের স্থান-কাল জ্যামিতি বর্ণনা করে থাকে।
One type of non-traversable wormhole metric is the Schwarzschild solution (see the first diagram):
আরও দেখুন
সম্পাদনাতথ্যসূত্র
সম্পাদনা- DeBenedictis, Andrew and Das, A. (২০০১)। "On a General Class of Wormhole Geometries"। Classical and Quantum Gravity। 18 (7): 1187–1204। arXiv:gr-qc/0009072 । ডিওআই:10.1088/0264-9381/18/7/304। বিবকোড:2001CQGra..18.1187D।
- Dzhunushaliev, Vladimir (২০০২)। "Strings in the Einstein's paradigm of matter"। Classical and Quantum Gravity। 19 (19): 4817–4824। arXiv:gr-qc/0205055 । ডিওআই:10.1088/0264-9381/19/19/302। বিবকোড:2002CQGra..19.4817D।
- Einstein, Albert and Rosen, Nathan (১৯৩৫)। "The Particle Problem in the General Theory of Relativity"। Physical Review। 48: 73। ডিওআই:10.1103/PhysRev.48.73। বিবকোড:1935PhRv...48...73E।
- Fuller, Robert W. and Wheeler, John A. (১৯৬২)। "Causality and Multiply-Connected Space-Time"। Physical Review। 128: 919। ডিওআই:10.1103/PhysRev.128.919। বিবকোড:1962PhRv..128..919F।
- Garattini, Remo (২০০৪)। "How Spacetime Foam modifies the brick wall"। Modern Physics Letters A। 19 (36): 2673–2682। arXiv:gr-qc/0409015 । ডিওআই:10.1142/S0217732304015658। বিবকোড:2004gr.qc.....9015G।
- González-Díaz, Pedro F. (১৯৯৮)। "Quantum time machine"। Physical Review D। 58 (12): 124011। arXiv:gr-qc/9712033 । ডিওআই:10.1103/PhysRevD.58.124011। বিবকোড:1998PhRvD..58l4011G।
- González-Díaz, Pedro F. (১৯৯৬)। "Ringholes and closed timelike curves"। Physical Review D। 54 (10): 6122–6131। arXiv:gr-qc/9608059 । ডিওআই:10.1103/PhysRevD.54.6122। বিবকোড:1996PhRvD..54.6122G।
- Khatsymosky, Vladimir M. (১৯৯৭)। "Towards possibility of self-maintained vacuum traversable wormhole"। Physics Letters B। 399 (3–4): 215–222। arXiv:gr-qc/9612013 । ডিওআই:10.1016/S0370-2693(97)00290-6। বিবকোড:1997PhLB..399..215K।
- Krasnikov, Serguei (২০০৬)। "Counter example to a quantum inequality"। Gravity and Cosmology। 46: 195। arXiv:gr-qc/0409007 । বিবকোড:2006GrCo...12..195K।
- Krasnikov, Serguei (২০০৩)। "The quantum inequalities do not forbid spacetime shortcuts"। Physical Review D। 67 (10): 104013। arXiv:gr-qc/0207057 । ডিওআই:10.1103/PhysRevD.67.104013। বিবকোড:2003PhRvD..67j4013K।
- Li, Li-Xin (২০০১)। "Two Open Universes Connected by a Wormhole: Exact Solutions"। Journal of Geometrical Physics। 40 (2): 154–160। arXiv:hep-th/0102143 । ডিওআই:10.1016/S0393-0440(01)00028-6। বিবকোড:2001JGP....40..154L।
- Morris, Michael S., Thorne, Kip S., and Yurtsever, Ulvi (১৯৮৮)। "Wormholes, Time Machines, and the Weak Energy Condition"। Physical Review Letters। 61 (13): 1446–1449। ডিওআই:10.1103/PhysRevLett.61.1446। পিএমআইডি 10038800। বিবকোড:1988PhRvL..61.1446M।
- Morris, Michael S. and Thorne, Kip S. (১৯৮৮)। "Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity"। American Journal of Physics। 56 (5): 395–412। ডিওআই:10.1119/1.15620। বিবকোড:1988AmJPh..56..395M।
- Nandi, Kamal K. and Zhang, Yuan-Zhong (২০০৬)। "A Quantum Constraint for the Physical Viability of Classical Traversable Lorentzian Wormholes"। Journal of Nonlinear Phenomena in Complex Systems। 9: 61–67। arXiv:gr-qc/0409053 । বিবকোড:2004gr.qc.....9053N।
- Ori, Amos (২০০৫)। "A new time-machine model with compact vacuum core"। Physical Review Letters। 95 (2)। arXiv:gr-qc/0503077 । ডিওআই:10.1103/PhysRevLett.95.021101। বিবকোড:2005PhRvL..95b1101O।
- Roman, Thomas, A. (২০০৪)। "Some Thoughts on Energy Conditions and Wormholes"। arXiv:gr-qc/0409090 [gr-qc]।
- Teo, Edward (১৯৯৮)। "Rotating traversable wormholes"। Physical Review D। 58 (2)। arXiv:gr-qc/9803098 । ডিওআই:10.1103/PhysRevD.58.024014। বিবকোড:1998PhRvD..58b4014T।
- Visser, Matt (২০০২)। "The quantum physics of chronology protection by Matt Visser"। arXiv:gr-qc/0204022 [gr-qc]। An excellent and more concise review.
- Visser, Matt (১৯৮৯)। "Traversable wormholes: Some simple examples"। Physical Review D। 39 (10): 3182–3184। arXiv:0809.0907 । ডিওআই:10.1103/PhysRevD.39.3182। বিবকোড:1989PhRvD..39.3182V।
বহিঃসংযোগ
সম্পাদনা- What exactly is a 'wormhole'? answered by Richard F. Holman, William A. Hiscock and Matt Visser.
- Why wormholes? by Matt Visser.
- Wormholes in General Relativity by Soshichi Uchii.
- White holes and Wormholes provides a very good description of Schwarzschild wormholes with graphics and animations, by Andrew J. S. Hamilton.
- Questions and Answers about Wormholes a comprehensive wormhole FAQ by Enrico Rodrigo.
- Large Hadron Collider – Theory on how the collider could create a small wormhole, possibly allowing time travel into the past.
- animation that simulates traversing a wormhole
- renderings and animations of a Morris-Thorne wormhole
- N.A.S.A's current theory on wormhole creation ওয়েব্যাক মেশিনে আর্কাইভকৃত ২৪ সেপ্টেম্বর ২০১৩ তারিখে