অম্পেয়্যারের বর্তনী সূত্র

SI পদ্ধতিতে অম্পেয়্যারের বর্তনী সূত্রটিকে সমাকলিত রূপে লেখা যায়

\oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I

অর্থাৎ B চৌম্বক ক্ষেত্রের বদ্ধ রেখা সমাকল (line integral) ঐ ক্ষেত্র দিয়ে অতিক্রান্ত তড়িৎপ্রবাহের সমানুপাতিক।

অম্পেয়্যারের বর্তনী সূত্রের প্রয়োগ

দীর্ঘ ঋজু তারের চৌম্বক ক্ষেত্র

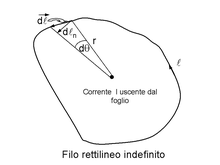
তারটিকে কেন্দ্র করে নির্দিষ্ট ব্যাসার্ধের বৃত্তীয় বদ্ধপথ নিয়ে এর উপরিস্থিত যে কোন ক্ষুদ্রাংশ নিলে চৌম্বক ক্ষেত্র সব স্থানেই ঐ ক্ষুদ্রাংশের সঙ্গে সমান্তরাল হয়।আবার প্রতিসাম্যের দরুন চৌম্বক ক্ষেত্রের মান বদ্ধপথটির প্রতিটি বিন্দুতেই সমান।

দীর্ঘ ঋজু সলিনয়েডের চৌম্বক ক্ষেত্র

এক্ষেত্রে চৌম্বক ক্ষেত্রের মান নির্ভর করে একক দৈর্ঘ্যের পাকসংখ্যার উপর, সলিনয়েডের পাকসংখ্যার উপর নয়।

সীমাবদ্ধতা

ম্যাক্সওয়েল প্রমাণ করেন অম্পেয়্যারের বর্তনী সূত্রটি শুধুমাত্র স্থির তড়িৎপ্রবাহের ক্ষেত্রেই প্রযোজ্য ।বদ্ধপথ দ্বারা পরিবেষ্টিত তড়িৎপ্রবাহ যদি সময়ের সঙ্গে সঙ্গে পরিবর্তিত হয়, তবে সূত্রটির ডানপক্ষে অতিরিক্ত পদ যোগ করতে হয়।যা তড়িচ্চুম্বকীয় ক্ষেত্র সমীকরণ নামে পরিচিত। ম্যাক্সওয়েল সংশোধন করে সূত্রটি বলেন $\oint _{\partial \Sigma }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I+\mu _{0}\varepsilon _{0}\iint _{\Sigma }{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathrm {d} \mathbf {S}$ অর্থাৎ $\oint _{\partial \Sigma }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I+\mu _{0}\varepsilon _{0}{\frac {d\Phi _{E}}{dt}}$ প্রকৃতপক্ষে ম্যাক্সওয়েল সরণ প্রবাহ নামে নতুন একটি রাশি বের করেন সেক্ষেত্রে মোট তড়িৎ এর পরিমাণ হবে সাধারণ তড়িৎ এবং ঐ সরণ প্রবাহ এর যোগফল এর সমান। অর্থাৎ $\oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}(I+I_{d})$

যেখানে $I_{d}=\mu _{0}\varepsilon _{0}{\frac {d\Phi _{E}}{dt}}$ হল ঐ সরণ প্রবাহ

আরও দেখুন

তথ্যসূত্র

প্রারম্ভিক পদার্থবিদ্যা - দোয়ারী মজুমদার মাইতি, ছায়া প্রকাশনী, দ্বাদশ শ্রেণি।